what is an computer algorithm
what is an computer algorithm
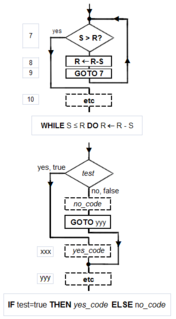Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO (
In computer systems, an algorithm is basically an instance of logic written in software by software developers, to be effective for the intended "target" computer(s) to produce output from given (perhaps null) input. An optimal algorithm, even running in old hardware, would produce faster results than a non-optimal (higher time complexity) algorithm for the same purpose, running in more efficient hardware; that is why algorithms, like computer hardware, are considered technology.
"Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This is true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is ... important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[42]
Unfortunately, there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example that uses Euclid's algorithm appears below.
Computers (and computors), models of computation: A computer (or human "computor"[43]) is a restricted type of machine, a "discrete deterministic mechanical device"[44] that blindly follows its instructions.[45] Melzak's and Lambek's primitive models[46] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[47] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[48]
Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[49] Minsky's machine proceeds sequentially through its five (or six, depending on how one counts) instructions, unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[50] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[51] Rarely must a programmer write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing completewith only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT. However, a few different assignment instructions (e.g. DECREMENT, INCREMENT, and ZERO/CLEAR/EMPTY for a Minsky machine) are also required for Turing-completeness; their exact specification is somewhat up to the designer. The unconditional GOTO is a convenience; it can be constructed by initializing a dedicated location to zero e.g. the instruction " Z ← 0 "; thereafter the instruction IF Z=0 THEN GOTO xxx is unconditional.
Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[52] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectivelyexecute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't, then the algorithm, to be effective, must provide a set of rules for extracting a square root.[53]
This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).
But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[54]When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" instruction available rather than just subtraction (or worse: just Minsky's "decrement").
Structured programming, canonical structures: Per the Church–Turing thesis, any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations, Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that, while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code", a programmer can write structured programs using only these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[55] Tausworthe augments the three Böhm-Jacopini canonical structures:[56] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[57] An additional benefit of a structured program is that it lends itself to proofs of correctness using mathematical induction.[58]
Canonical flowchart symbols[59]: The graphical aide called a flowchart, offers a way to describe and document an algorithm (and a computer program of one). Like the program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only four: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm–Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles, but only if a single exit occurs from the superstructure. The symbols, and their use to build the canonical structures are shown in the diagram.
By....
What is a Computer Algorithm? -
Algorithm?
Consider how you use a computer in a typical day. For example, you start working on a report, and once you have completed a paragraph, you perform a spell check. You open up a spreadsheet application to do some financial projections to see if you can afford a new car loan. You use a web browser to search online for a kind of car you want to buy.
You may not think about this very consciously, but all of these operations performed by your computer consist of algorithms. An algorithm is a well-defined procedure that allows a computer to solve a problem. Another way to describe an algorithm is a sequence of unambiguous instructions. The use of the term 'unambiguous' indicates that there is no room for subjective interpretation. Every time you ask your computer to carry out the same algorithm, it will do it in exactly the same manner with the exact same result.
Consider the earlier examples again. Spell checking uses algorithms. Financial calculations use algorithms. A search engine uses algorithms. In fact, it is difficult to think of a task performed by your computer that does not use algorithms.
How Do Algorithms Work?
Let's take a closer look at an example.
A very simple example of an algorithm would be to find the largest number in an unsorted list of numbers. If you were given a list of five different numbers, you would have this figured out in no time, no computer needed. Now, how about five million different numbers? Clearly, you are going to need a computer to do this, and a computer needs an algorithm.
Below is what the algorithm could look like. Let's say the input consists of a list of numbers, and this list is called L. The number L1 would be the first number in the list, L2 the second number, etc. And we know the list is not sorted - otherwise, the answer would be really easy. So, the input to the algorithm is a list of numbers, and the output should be the largest number in the list.
The algorithm would look something like this:
Step 1: Let Largest = L1
This means you start by assuming that the first number is the largest number.
Step 2: For each item in the list:
This means you will go through the list of numbers one by one.
Step 3: If the item > Largest:
If you find a new largest number, move to step four. If not, go back to step two, which means you move on to the next number in the list.
Step 4: Then Largest = the item
This replaces the old largest number with the new largest number you just found. Once this is completed, return to step two until there are no more numbers left in the list.
Step 5: Return Largest
This produces the desired result.
Notice that the algorithm is described as a series of logical steps in a language that is easily understood. For a computer to actually use these instructions, they need to be written in a language that a computer can understand, known as a programming language.
**2nd ...##
Flowchart examples of the canonical Böhm-Jacopini structures: the SEQUENCE (rectangles descending the page), the WHILE-DO and the IF-THEN-ELSE. The three structures are made of the primitive conditional GOTO ({{{1}}}) (a diamond), the unconditional GOTO (rectangle), various assignment operators (rectangle), and HALT (rectangle). Nesting of these structures inside assignment-blocks result in complex diagrams (cf Tausworthe 1977:100, 114)."Elegant" (compact) programs, "good" (fast) programs : The notion of "simplicity and elegance" appears informally in Knuth and precisely in Chaitin:
- Knuth: " … we want good algorithms in some loosely defined aesthetic sense. One criterion … is the length of time taken to perform the algorithm …. Other criteria are adaptability of the algorithm to computers, its simplicity and elegance, etc"[40]
- Chaitin: " … a program is 'elegant,' by which I mean that it's the smallest possible program for producing the output that it does"[41]
Algorithm versus function computable by an algorithm: For a given function multiple algorithms may exist. This is true, even without expanding the available instruction set available to the programmer. Rogers observes that "It is ... important to distinguish between the notion of algorithm, i.e. procedure and the notion of function computable by algorithm, i.e. mapping yielded by procedure. The same function may have several different algorithms".[42]
Unfortunately, there may be a tradeoff between goodness (speed) and elegance (compactness)—an elegant program may take more steps to complete a computation than one less elegant. An example that uses Euclid's algorithm appears below.
Computers (and computors), models of computation: A computer (or human "computor"[43]) is a restricted type of machine, a "discrete deterministic mechanical device"[44] that blindly follows its instructions.[45] Melzak's and Lambek's primitive models[46] reduced this notion to four elements: (i) discrete, distinguishable locations, (ii) discrete, indistinguishable counters[47] (iii) an agent, and (iv) a list of instructions that are effective relative to the capability of the agent.[48]
Minsky describes a more congenial variation of Lambek's "abacus" model in his "Very Simple Bases for Computability".[49] Minsky's machine proceeds sequentially through its five (or six, depending on how one counts) instructions, unless either a conditional IF–THEN GOTO or an unconditional GOTO changes program flow out of sequence. Besides HALT, Minsky's machine includes three assignment (replacement, substitution)[50] operations: ZERO (e.g. the contents of location replaced by 0: L ← 0), SUCCESSOR (e.g. L ← L+1), and DECREMENT (e.g. L ← L − 1).[51] Rarely must a programmer write "code" with such a limited instruction set. But Minsky shows (as do Melzak and Lambek) that his machine is Turing completewith only four general types of instructions: conditional GOTO, unconditional GOTO, assignment/replacement/substitution, and HALT. However, a few different assignment instructions (e.g. DECREMENT, INCREMENT, and ZERO/CLEAR/EMPTY for a Minsky machine) are also required for Turing-completeness; their exact specification is somewhat up to the designer. The unconditional GOTO is a convenience; it can be constructed by initializing a dedicated location to zero e.g. the instruction " Z ← 0 "; thereafter the instruction IF Z=0 THEN GOTO xxx is unconditional.
Simulation of an algorithm: computer (computor) language: Knuth advises the reader that "the best way to learn an algorithm is to try it . . . immediately take pen and paper and work through an example".[52] But what about a simulation or execution of the real thing? The programmer must translate the algorithm into a language that the simulator/computer/computor can effectivelyexecute. Stone gives an example of this: when computing the roots of a quadratic equation the computor must know how to take a square root. If they don't, then the algorithm, to be effective, must provide a set of rules for extracting a square root.[53]
This means that the programmer must know a "language" that is effective relative to the target computing agent (computer/computor).
But what model should be used for the simulation? Van Emde Boas observes "even if we base complexity theory on abstract instead of concrete machines, arbitrariness of the choice of a model remains. It is at this point that the notion of simulation enters".[54]When speed is being measured, the instruction set matters. For example, the subprogram in Euclid's algorithm to compute the remainder would execute much faster if the programmer had a "modulus" instruction available rather than just subtraction (or worse: just Minsky's "decrement").
Structured programming, canonical structures: Per the Church–Turing thesis, any algorithm can be computed by a model known to be Turing complete, and per Minsky's demonstrations, Turing completeness requires only four instruction types—conditional GOTO, unconditional GOTO, assignment, HALT. Kemeny and Kurtz observe that, while "undisciplined" use of unconditional GOTOs and conditional IF-THEN GOTOs can result in "spaghetti code", a programmer can write structured programs using only these instructions; on the other hand "it is also possible, and not too hard, to write badly structured programs in a structured language".[55] Tausworthe augments the three Böhm-Jacopini canonical structures:[56] SEQUENCE, IF-THEN-ELSE, and WHILE-DO, with two more: DO-WHILE and CASE.[57] An additional benefit of a structured program is that it lends itself to proofs of correctness using mathematical induction.[58]
Canonical flowchart symbols[59]: The graphical aide called a flowchart, offers a way to describe and document an algorithm (and a computer program of one). Like the program flow of a Minsky machine, a flowchart always starts at the top of a page and proceeds down. Its primary symbols are only four: the directed arrow showing program flow, the rectangle (SEQUENCE, GOTO), the diamond (IF-THEN-ELSE), and the dot (OR-tie). The Böhm–Jacopini canonical structures are made of these primitive shapes. Sub-structures can "nest" in rectangles, but only if a single exit occurs from the superstructure. The symbols, and their use to build the canonical structures are shown in the diagram.
By....
